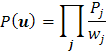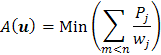Metody řešení
krystalových struktur
Jindřich Hašek – František Pavelčík
1. ÚVOD
1.1 Formulace problému.
1.2 Snížení vlivu tepelného pohybu atomů
1.3 Výpočet strukturních faktorů pro
bodovou strukturu
1.4 Dělení metod řešení krystalových
struktur
2. METODY ZALOŽENÉ
NA INTERPRETACI PATTERSONOVY
FUNKCE
2.1 Využití symetrie při interpretaci Pattersonovy funkce
2.2 Superpoziční metody
2.3 Dekonvoluce Pattersonovy funkce
s využitím znalosti molekulárního fragmentu
3. PŘÍMÉ METODY ŘEŠENÍ
FÁZOVÉHO PROBLÉMU
3.1 Určení hodnot
seminvariantů
3.2 Fixace počátku
souřadnicové soustavy
3.3 Výpočet fází
strukturních faktorů
4. METODA ANOMÁLNÍHO ROZPTYLU A METODA IZOMORFNÍHO NAHRAZENÍ
5. ITERATIVNÍ
METODY ŘEŠENÍ KRYSTALOVÝCH
STRUKTUR
5.1 Metody optimalizace funkce popisující shodu modelu
a experimentu
5.2 Metody opakované Fourierovy transformace
5.3 Molekulární grafika
6. EXPERIMENTÁLNÍ URČENÍ
FÁZÍ STRUKTURNÍCH FAKTORŮ
7. JEDNOZNAČNOST URČENÍ
KRYSTALOVÉ STRUKTURY
___________________________________________________________________________________
1.
ÚVOD
1.1 Formulace problému
Třírozměrný obraz (1) krystalové
struktury (2), reprezentovaný
třírozměrnou mapou elektronové
hustoty (3), nebo mapou hustoty magnetického momentu (4)
v základní buňce, je možno získat Fourierovou transformací (5):
kde sčítání probíhá přes
všechny difrakční vektory H ležící uvnitř měřené koule (6). Grafické znázornění funkce (g1) nazýváme
obvykle Fourierovou mapou (7). Strukturní faktory (8) 
jsou komplexní veličiny definované
Fourierovou transformací
inverzní k transformaci (g1)
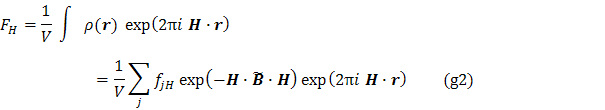
kde
V je objem základní buňky, r
je polohový vektor (9), 
je tenzor teplotních kmitů (10) j- teho atomu, a atomový rozptylový faktor 
(11) udává závislost
toku záření rozptýleného j – tým atomem na difrakčním úhlu, který je pro daný krystal
a použitý druh záření jednoznačně určen difrakčním vektorem H (12).
Přímému
výpočtu obrazu struktury podle vztahu (g1) brání to, že neznáme fáze strukturních faktorů (13). Tyto mohou být sice určeny
experimentálně (viz kap. F), ale v praxi tento postup naráží na
řadu potíží. Proto jsou v naprosté většině
případů fáze určovány výpočtem – řešení fázového problému (14).
Protože vztah (g1) dává pro tentýž soubor 
nekonečné množství možných reálných
funkcí r(r),
je třeba k nalezení správného řešení využít apriorní strukturní informace (15), tj. informace o rozložení struktury, nezápornosti elektronové hustoty (16) atd. Čím je více těchto informací
aktivně použito, tím účinnější je metoda.
Společným
rysem všech
metod řešení fázového problému je snaha co nejvíce zjednodušit
v první fázi výpočtu model
strutury (17). Pomocí ab initio metod (18), které
nevyžadují znalost části struktury, je obvykle určena pouze poloha
některých význačných atomů, majících rozhodující vliv na
difrakci záření. Na základě tohoto strukturního fragmentu (19) je
určen zbytek struktury. Takto určený hrubý model struktury, tj.
polohy atomů a celkový
izotropní teplotní parametr (20) pak
může být zjemněn použitím většího počtu nastavitelných
parametrů (polohy vodíkových atomů, anizotropní teplotní parametry (21),
obsazovací faktory (22), parametry atomových orbitalů (23) atd.), a rozdíly mezi měřenými
a vypočtenými intenzitami reflexí jsou minimalizovány některou
z metod minimalizace
vícerozměrných funkcí (24). Tyto metody
jsou popsány v kapitole „Upřesnění strukturních parametrů“.
Strukturní amplitudy (25), tj. absolutní hodnoty (26), či velikosti (27)
strukturních faktorů (viz komentář) jsou obvykle počítány
za předpokladu, že měřený vzorek je ideální mozaikový krystal (28). Potom, po
odstranění příspěvku od vícenásobné
difrakce (29) po korekci na primární a sekundární extinkci (30), po odečtení příspěvku tepelného difuzního rozptylu (31), po korekci
na Lorentzův faktor (32), polarizační
faktor (33) a absorpční faktor (34) a po
odstranění některých
dalších nežádoucích vlivů uspořádaní difrakčního experimentu, jsou úměrné druhé mocnině
měřených intenzit.
Účinnost
všech metod řešení krystalových struktur je tím větší, čím
jednodušší je hledaný model struktury. Proto se všechny metody snaží
o výpočet takových strukturních faktorů, které by odpovídali
idealizované struktuře, v níž by byli jednotlivé atomy nahrazeny
nekmitajícími body.
1.2 Snížení vlivu teplotního pohybu atomů
Celkový teplotní parametr
aproximující jedním číslem (nebo tenzorem ) tepelný pohyb všech atomů
v základní buňce, a škálový
faktor (35)¸ který převádí strukturní
faktory na absolutní škálu (36) (v jednotkách
elektronové hustoty nebo magnetického momentu), bývají spravidla
určeny pomocí Wilsonova grafu (37), z
K – křivky (38) nebo z Debyeovy funkce (39).
Vydělením strukturních faktorů teplotním
faktorem (40), aproximovaným výrazem 
dostáváme strukturní faktory idealizované
struktury s nekmitajícími atomy (41).
1.3 Výpočet strukturních faktorů pro bodovou strukturu
V případě,
že se hledaný model struktury skládá
z bodových atomů (42), lze v principu provést stanovení krystalové struktury (43) bez dalších předběžných informací
o struktuře.
Účinnost
řešení fázového problému dále podstatně vzroste, pracujeme-li s modifikovanými strukturními faktory (44), jimž zodpovídá zostřená Fourierova mapa (45)
s ostrými a dobře rozlišitelnými maximy. Modifikace strukturních
faktorů tak, aby odpovídali bodové
struktuře (46) je
umožněno tím, že atomové rozptylové křivky atomů všech typů
dávají po vydělení počtem jejich elektronů v prvním
přiblížení tutéž křivku, nazývanou tvarová funkce (47). Podle
způsobu aproximace tvarového faktoru jsou užívány jednotkové strukturní faktory (48)
kde 
je strukturní faktor pro difrakční
vektor H ş
(0, 0, 0), nebo normalizované strukturní faktory (49)
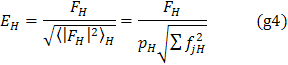
kde
je statistická váha reflexe
(50). Fourierova mapa, v níž jsou
koeficienty 
nahraženy normalizovanými strukturními
faktory 
je nazývaná
E – mapou (51). Pokud jsou střední hodnoty 
pro různé paritní skupiny reflexí (52)
podstatně rozdílné, bývá provedena renormalizace
strukturních faktorů (53) tak, aby
v každé skupině bylo 
1.4 Dělení metod řešení krystalových
struktur
Metody řešení
krystalových struktur lze rozdělit do čtyř skupin:
A Vektorové
(Pattersoovy) metody (54) řeší fzový problém ve vektorovém prostoru (55), zpravidla pomocí Pattersonovy funkce (56)¸ kterou lze vypočítat bez znalosti strukturních faktorů
Správné řešení je hledáno podle shody mezi
množinou meziatomových vektorů (57) modelu struktury a množinou polohových
vektorů maxim na Pattersonově funkci.
B Přímé metody (58),
u nichž je apriorní strukturní informace převedena Fourierovou
transformací do vztahů mezi strukturními faktory, nazývaných fázové
relace (59). Tyto relace umožňují
určení fází přímo z amplitud strukturních faktorů bez
výpočtu Pattersonovy funkce. Mezi tyto metody bývá řazena též metoda
maximální entropie (60).
C Metody
využívající značeného vektoru (61)
a opakovaného měření intenzit difraktovaného záření
při změněné rozptylvé schopnosti malé části struktury. Této
změny je dosahováno
a) změnou vlnové délky použitého
záření tak, aby došlo k podstatné změně rozptylové
schopnosti atomů určitého typu – metoda
anomálního rozptylu (62).
b) záměnou některého atomu
ve struktuře tak, aby přitom nedošlo k příliš velké
změně krystalové struktury – metoda
izomorfního nahrazení (63).
D Iterační metody
(64), které na základě známých poloh
některých atomů určí polohy všech zbylých atomů struktury
v jednom nebo více cyklech.
E Metody
experimentálního určení fází strukturních faktorů.
2. METODY
ZALOŽENÉ NA
INTERPRETACI PATTERSONOVY FUNKCE
Vektorové metody se snaží
identifikovat autokonvolucí (65) strukturního motivu ve vektorovém prostoru
nějaké funkce podobné Pattersonové funkci. Často bývá užíváno zostřené Pattersonovy funkce (66), s odstraněným maximem v počátku (67). Jsou užívány též další modifikace
odstraňující maxima již známých atomů, zlepšující poměr signál/šum (68), atd.
Prostorovou grupu Pattersonovy funkce získáme z prostorové grupy
krystalové struktury nahrazením operací symetrie obsahujících translaci
odpovídajícími operacemi symetrie bez této translace a přidáním
středu symetrie. Prostorová grupa Pattersonovy funkce je tedy symorfní
grupa izogonální s prostoovou grupou krystalu.
2.1
Využití symetrie při interpretaci Pattersonovy funkce.
Maxima Pattersonovy funkce odpovídající
vektorům mezi vzájemně symetricky sdruženými atomy leží na Harkerových řezech (69), resp.Harkerových
přímkách (70). Maxima na Hakerových
řezech mohou být interpretována buď přímo numericky, nebo
prostřednictvím implikační
transformace (71) Harkerových řezů
do implikačních diagramů (72). Satelitní
maxima (73) na Pattersonově funkci nebo
na implikačním diagramu slouží k potvrzení prostorové grupy. Spojením
informací ze všech možných implikačních diagramů je možné vytvořit
spojité vícenácsobné
implikační funkce (74), z nichž nejznámejší je symetrická
minimová funkce (75) 
, kde 
jsou operátory symetrie. Maxima této funkce
odpovídají přímo polohám atomů. Řešení struktury usnadňuje
přítomnost těžkých atomů (76) nebo
charakteristických skupin atomů dávajících snadno interpretovatelná
maxima.
2.2 Superpoziční metody
Rozsáhlou třídu vektorových
metod tvoří superpoziční (koincidenční) metody (77),
které jsou založeny na hledání shody mezi vzájemně posouvanými
Pattersonovými funkcemi nebo mezi Pattersonovou funkcí a vyhledávací funkcí (78),
kterou lze obvykle interpretovat jako autokonvoluci modelu strukturního
fragmentu. Kritérium shody bývá vysoká hodnota vážené, či nevážené:
|
součtové funkce (79) |
|
(g6) |
|
součinové funkce (79) |
|
(g7) |
|
minimové funkce (79) |
|
(g8) |
|
funkce nejmenšího průměru
(80) |
|
(g9) |
řádu n , kde
je hodnota Pattersonovy funkce v bodě j – teho
vektoru, sčítáva
se přes m <
n nejmenších
hodnot /wj z celkového
počtu n vektorů funkce
vyhledávající obraz a 
je váha připisována j –
tému vektoru.
Pokud při superpozici posouváme Pattersonovou funkci
o libovolný meziatomový vektor, mluvíme o vektorové superpozici (81). Když je
poloha jednoho atomu vzhledem k prvkům symetrie známá, tak se
superpozice s posunem počátku Pattersonovy funkce o polohový
vektor atomu a jeho symetrických ekvivalentů nazývá atomová superpozice (82). Symetrie krystalu se při atomové superpozici
zachovává.
2.3 Dekonvoluce Pattersonovy funkce
s využitím znalosti molekulárního fragmentu
Stanovení krystalové struktury je
obvykle děleno do dvou částí. Nejprve je nalezena orientace fragmentu
pomocí rotační funkce (83), a potom je hledáno jeho umístění
vůči prvům symetrie nebo vůči známé části
struktury pomocí translační funkce (84). Je přitom využíváno faktu, že
meziatomové vektory lze podle jejich velikosti rozdělit na intrafragmentální a interfragmentální vektory (85) nesoucí informaci o orientaci, resp.
umístění fragmentu.
Při
výpočtu je použito vzorkování (86) Pattersonovy funkce, což znamená, že tuto
funkci popíšeme jejími hodnotami v bodech sítě, která má vhodně
volenou velikost oka sítě (87) tak, aby nebylo nebezpečí vynechání
některého maxima, ale přitom aby byl počet bodů co
nejmenší.
Shodná orientace strukturních fragmentů odpovídá některému z nejvyšších maxim na rotační funkci, např.
kde P(x) je hodnota Pattersonovy funkce v bodě x , a 
je hodnota autokonvoluce modelu části
struktury nebo Pattersonova funkce již známé struktury izomorfní (88) se strukturou zkoumaného krystalu
v bodě y. U malých molekul je výhodnější provést
výpočet v reciprokém prostoru
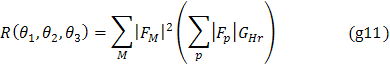
kde sčítání probíhá přes daleko menší počet bodů než je vzorkovacích
bodů v prostoru Pattersonovy funkce. 
je interferenční
funkce pro kouli (89) o poloměru r.
Z početních
důvodů je vhodné vyjádřit rotační funkci pomocí sférických funkcí (90)
a Pattersonovu funkci popsat v bodech ležících na
soustředěných kruhových plochách a vyhovujících symetrii
příslušné bodové grupy. Protože výpočet proběhne takto rychleji,
je takto vyjádřena funkce nazývaná rychlou
rotační funkcí (91).
Vzájemná
rotace molekul bývá vyjádřená buď prostředníctvím Eulerových úhlů (92) 
nebo sférických
úhlů (93) 
. Zobrazení v prostoru
Eulerových úhlů nebo sférických úhlů volíme podle symetrie problému.
Obdobně
i translační funkci lze vyjádřit různými způsoby jak
v přímém, tak i v reciprokém prostoru. Protože
u translační funkce bývá kritérium shody vyjádřeno přímo
pomocí fází strukturních faktorů, bývá tato funkce řazena mezi
přímé metody. Poloha nejvyššího maxima na translační funkci udává
pravděpodobný vektor posunutí (94) molekulárního fragmentu známé orientace do
správné polohy vůči prvkům symetrie, resp. vůči již
známé části struktury. Pokud techniku rotační a translační
funkce aplikujeme obecně na struktury biopolymerů a použijeme-li
známý molekulární fragment podobné struktury, mluvíme o metodě molekulárního nahrazení (95).
V případě,
že jeden atom struktury vykazuje anomální rozptyl, je vhodné použít
k řešení imaginární části Pattersonovy funkce tzv. sinusové syntézy (96)
dávající za jistých podmínek maxima v polohách
atomů překrytá jejich obrazem vzniklým zobrazením přes
střed antisymetrie (97) v počátku.
Perspektivní,
ale z matematického hlediska obtížné, je využití šestirozměrné dvojité Pattersonovy funkce (98)
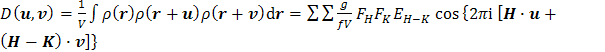(g13)
Četné další
aplikace Pattersonovy
funkce lze najít ve speciálních Fourierových syntézách užívaných při
iteračním zpřesňování již částečně známé
struktury a ve spojitosti s metodami izomorfního nahrazení a anomálního
rozptylu.
3. PŘÍMÉ
METODY ŘEŠENÍ
FÁZOVÉHO PROBLÉMU
Přímými metodami
řešení krystalových struktur jsou nazývány
metody určující fáze strukturních faktorů přímým výpočtem z amplitud strukturních faktorů 
bez použití funkcí Pattersonova
typu. Protože však fáze nelze vypočítat, dokud není fixována poloha
struktury vůči počátku
souřadnicové soustavy, byly definovány následující pojmy:
Univerzální strukturní invariant (99) je lineární kombinace fází (struturních
faktorů), která nezávisí na tom, jakým spůsobem umístníme
počátek souřadnicového systému vůči struktuře.
Strukturní seminvariant (100) je lineární kombinace fází,
která se nemění při takových změnách umístění počátku,
při nichž se nemění jeho poloha vůči prvkům symetrie
prostorové grupy.
N-fázový invariant (101) je funkce N symetricky
nezávislých fází taková, že její funkční hodnota nezávisí na umístění
počátku.
N-fázový seminvariant (102) je funkce N symetricky
nezávislých fází taková, že její funkční hodnota nezávisí na
změně počátku, která zachovává jeho polohu vůči všem
prvkům symetrie prostorové grupy.
Postup
přímých metod lze rozdělit na tři části
a) Určení seminvariantů
a výpočet jejich hodnot
b) Fixace počátku souřadnicové
soustavy
c) Výpočet fází a identifikace
správného řešení
3.1
Určení hodnot seminvariantů
Hlavním výsledkem
teorie nerovností (103)
vycházející z nezápornosti
elektronové hustoty je pravidlo o nezápornosti Karleova – Hauptmanova determinantu (104) 
. Je-li při vytváření
matice D maximálně využito symetrie prostorové grupy, je tato matice
nazývaná Goedkoopovou maticí (105). Bezprostředním důsledkem
nezápornosti Karleova – Hauptmanova determinantu
nízkého řádu (106) jsou Harkerovy – Kasperovy nerovnosti (107).
Mnohem účinnější než nerovnosti jsou statistické metody (108)
založené na předpokladu rovnoměrného rozložení atomů
v základní buňce. Základem k odvození statistických relací (109) je
výpočet sdružené hustoty
pravděpobnosti (110) pro zvolenou
množinu strukturních faktorů. Z praktických důvodů je
často užíváno podmíněné
hustoty pravděpodobnosti (111)
předpokládající konstantní hodnoty některých amplitud nebo fází.
Jsou-li některé amplitudy či fáze neznámé, bývá užito marginální hustoty pravděpodobnosti (112). Hustota pravděpodobnosti bývá
vyjádřena buď pomocí rozvoje funkce
generující kumulanty (113) do Gramovy – Charlierovy řady (114) nebo do Edgeworthovy
exponenciální řady (115). Pro centrické seminvarianty (116) resp. acentrické
seminvarianty (117) je distribuční funkce (118)
popsána prostřednictvím Hermitových
polynomů (119) resp.
Laguerrových polynomů (120), kde proměnnou jsou amplitudy
strukturních faktorů.
Definujeme-li řád strukturního invariantu t (121) jako počet fází, které jej vytváří, klesá jeho příspěvek
k určení distribuce s koeficientem 
. Řád fázové relace (122) je
definován jako nejnižší řád nenulového
smíšeného momentu (123), který v relaci
vystupuje. Výběr strukturních faktorů dávajících distribuční
funkci s nejvyšším obsahem strukturní informace je dán teorii reprezentací (124). První reprezentaci seminvariantu (125) řádu τ tvoří všechny strukturní invarianty řádu τ + 2, které umožňují přímé
určení tohoto seminvariantu.
Sdruženými amplitudami (126) této reprezentace jsou všechny amplitudy
v ní vystupující s výjimkou bazálních
amplitud (127), tj. amplitud, které
odpovídají fázím, pro které je distribuce počítána. Účinnost fázové
relace klesá s řádem této relace a roste s počtem
sdružených amplitud.
Takto odvozené distribuční funkce nejsou přesné
kvůli:
-
zvlnění způsobenému
ukončením řady (128), do které je funkce rozvinuta
-
neoprávněnosti předpokladu rovnoměrného rozložení (129)
atomů v asymetrické části základní buňky
-
zanedbání korelaci (130) a nahrazení sdružené mnohodimenzionální
distribuce přímým součinem (131) marginálních distribucí s malou bází (132).
Přesnějším postupem
umožňujícím plné využití apriorní strukturní informace je metoda maximální entropie (133).
Nejužívanější distribucí je distribuce hodnot tripletů 
a distribuce
kvartetů (134)
.
Relace určující hodnotu jednofázového strukturního seminvariantu na
základě reflexí typu H(R – I) se nazývá 
relace (135). Relace určující hodnotu fáze vystupujíci
současně v několika tripletech se nazývá 
relace (136).
Nejznámějším
důsledkem mnoharozměrných distribucí je pravidlo maximálního determinantu (137),
který říká, že nejpravděpodobnejší hodnoty fází odpovídají nejmenším vlastním hodnotám (138)
Karleovy – Hauptmanovy matice (139).
Z distribučních
funkcí byly též odvozeny vztahy pro střední hodnoty některých
seminvariantů, které tvoří základ algebraických relací (140). Tyto vztahy
lze psát ve tvaru
seminvariant = funkce
středních hodnot amplitud.
Nejdůležitejší „přesnou relací“ je Sayreova rovnice (141)
kde 
označuje střední hodnotu (142) a difrakční
vector K
běží přes
celý reciproký prostor. Ze Sayreovy
rovnice vyplývá bezprostředně tangentová
formule (vzorec) (143)
která je nejčastěji užívaným vztahem
v přímých metodách.
3.2 Fixace počátku souřadnicové
soustavy
Jen u deseti prostorových grup
je počátek souřadnicové
soustavy (144) definován
jednoznačně svou polohou vůči prvkům symetrie.
V ostatních případech je vždy uvnitř třídy symetricky ekvivalentních počátků (145) konečný, nebo nekonečný počet
dalších možných umístění počátku se stejným prostorovým
uspořádaním prvků symetrie kolem sebe. U vektorových metod je volba počátku (146)
provedena přímo umístěním strukturního fragmentu. U přímích
metod však mluvíme o fixaci
počátku (147) protože zde volbou fází
vhodných reflexí pouze fixujeme polohu struktury vůči počátku
v nějakém předem neznámém místě.
Protože lineární kombinace (148) difrakčních vektorů 
reflexí
vytvářejících seminvariant 
tvoří v reciprokém prostoru translační
podgrupu, bývá často podmínka pro seminvariant
vyjádřena pomocí kongruenci (149). Strukturní seminvariant (invariant) je tak
definován jako lineární kombinace fází, jíž odpovídající lineární kombinace
difrakčních vektorů 
je rovna vektoru H,
jemuž seminvariantně
(resp. invariantně)
sdružený vektor (150) 
je kongruentní s nulovým vektorem (151)
podle seminvariantního (invariantního) modulu (152) 
mod 
.
Je-li to nutné, je jedna
z možných enantiomorfních forem
struktury fixována tím, že
držíme beze změny strukturní invariant, o němž
víme, že není 0 nebo
π a že vystupuje v mnoha
spolehlivých fázových relací
uvnitř intervalu (0, π). Vyžaduje-li to daná
prostorová grupa, je počátek souřadnicové soustavy fixován volbou některé
z možných hodnot jedné až tří fází vybraných podle následujících výběrových pravidel (153)
-
soubor seminvariantně sdružených difrakčních
vektorů musí splňovat podmínku lineární nezávislosti podle modulu (154).
-
soubor vektorů HS musí dále
splňovat podmínku primitivnosti
podle modulu (155), aby byla zajištěna přístupnost (156)
libovolné fáze prostřednicvím fázových relací , tj. aby byl libovolný
vektor H racionálně
závislý (157) na seminvariantně
sdružených vektorech fází fixujících počátek podle modulu .
Většina
metod řešení fázového problému vychází při řešení z počátečního souboru fází (158), který obsahuje fáze reflexí fixujících
počátek a enantiomorfní formu a další fáze, které se vyskytují
v mnoha fázových relacích a umožňují určení všech ostatních
fází v malém počtu kroků.
Fáze obecných (acentrických) reflexí (159) mohou být voleny libovolně. Fáze speciálních reflexí (160) mohou nabývat jen několika diskrétních hodnot,
např. 0, ±(π/2), π . Fáze centrických reflexí (161)
mohou nabývat pouze hodnot 0
a π . Odpovídající projekce
struktury podél difrakčního vektoru má střed symetrie.
3.3 Výpočet fází strukturních faktorů
Plně obecnou metodou je metoda vyrovnávání distribucí seminvariantů (162), která určuje fáze (strukturních
faktorů) na základě statistických testů shody (163) mezi teoretickými (164)
a empirickými distribucemi
seminvariantů (165).
Ostatní metody jsou založeny na
řešení přeurčené soustavy
lineárních (nebo nelineárních) rovnic (166),
tvořených fázovými relacemi, podmínkami pro fixaci počátku
a případně dalšími vazbovými podmínkami mezi hledanými fázemi.
Protože však fázové relace jsou pouze vyjádřením pravděpodobné
hodnoty seminvariantů, je každá z nich zatížena chybou , která roste
s velikostí struktury a řešení se stává obtížné.
Řešení regulární soustavy rovnic (167)
často nevede ke správnému výsledku a proto řešení bývá
často formulováno jako minimalizace vhodné účelové funkce (168), jejíž
hodnota závisí na rozdílech mezi pravými a levými stranami
mnohonásobně většího počtu fázových relací, než je
určovaných fází. Správné řešení však spravidla neodpovídá globálnímu minimu (169)
a je jej třeba hledat mezi nejnižšími lokálními minimy (170), nebo do
účelové funkce zahrnout další omezující
podmínky (171). Tyto metody vedou ke
správnému řešení bez problému, jen když je graf spolehlivých seminvariantů (172)
souvislý (173) a má vysoký hranový
(174) i uzlový
stupeň souvislosti (175).
Nejužívanější metodou
výpočtu fází je metoda mnoha řešení
(176), v níž jsou fixovány fáze ve
startovacím souboru a fáze zbylých reflexí jsou vypočítány
v několika cyklech ze spolehlivých fázových relací. Tento postup
ovšem musí být opakován, dokud se nepodaří odhadnout fáze ve startovacím
souboru dostatečně blízko správnému řešení. Výběr reflexí
do startovacího souboru je prováděn tak, aby orientovaný graf spolehlivých fázových relací (177),
v jehož nulté hladině jsou právě startovací fáze, měl
co nejmenší počet hladin ve své hladinové
struktuře (178). Z neiteračních
metod částečně splňujících tento požadavek, lze uvést
výběr reflexí z konce konvergenční
mapy (179).
Vyšší počet fází
v počátečním souboru vede ke snížení počtu hladin grafu
fázových relací, a tedy ke spolehlivější metodě. Toho využívá metoda magických čísel (180),
která zvyšuje počet fází v počátečním souboru zavedením
přibližně splnitelných vazbových podmínek mezi fázemi uvnitř
startovacího souboru.
K nalezení správného řešení
mezi velkým počtem zkušebních
souborů fází (181) byla vyvinuta řada testů spolehlivosti (182). Tyto
testy jsou sami o sobě vysoce nespolehlivé, protože obvykle zkoumají pouze
shodu jediné charakteristiky mezi teoretickými a empirickými distribucemi.
Proto bývají sdruženy do jediného kombinovaného
testu spolehlivosti (183), který indikuje
správné řešení s vysokou pravděpodobností.
Metoda symbolické adice (184) se od metody mnoha
řešení liší tím, že jsou v ní do startovacího souboru fází dosazeny
místo číselných hodnot symbolické
fáze (symboly) (185). Optimální hodnoty
symbolických fází jsou nalezeny obdobnými testy jako u metod mnoha
řešení. Velkým handicapem symbolické adice je, že symboly umožňují
použití pouze nepřesného součtového
vzorce (186)
a i v tomto případě
dochází díky periodicitě fází 2π k problémům
při určení průměrné
hodnoty na pravé straně vztahu
(g16). Konečným kriteriem správnosti zkušebního souboru fází je však vždy
nalezení správného strukturního fragmentu na odpovídající E
mapě.
4. METODA
ANOMÁLNÍHO ROZPTYLU
A METODA IZOMORFNÍHO
NAHRAZENÍ
Metoda izomorfního nahrazení je
nejúčinnějším postupem k řešení krystalových struktur
makromolekulárních látek. Je založena na porovnávání měření dvou
struktur, které se o sebe liší jen rozptylovou schopností malého
počtu těžkých atomů s přibližně známou polohou. Protože fáze strukturních faktorů původní (přirozené)
struktury (187)
a odvozené struktury (188) nejsou známé, jsou obrazem vzájemně si
odpovídajících strukturních faktorů v komplexní rovině (189) dvě
kružnice, jejichž středy jsou vzájemně posunuté o známý
značený vektor. Protože se tyto kružnice obecně protínají ve dvou
bodech, úloha určení fází není jednoznačně řešitelná jen na
základě jedné izomorfní struktury (190). Tato dvojznačnost v určení
fází může být řešena proměřením další izomorfně substituované struktury (191)
s těžkým atomem na jiném místě -
metoda vícenásobného izomorfního
nahrazení (192), nebo kombinací metody
izomorfního nahrazení s metodou anomálního rozptylu. (SIRAS metoda (193))
U metody anomálního rozptylu (194) je
vhodnou změnou vlnové délky záření dosažena velká změna
rozptylové schopnosti vybraných atomů struktury. Tím získáme obdodu
měření na dvou „zaručeně“ izomorfních strukturách
a lze použít metody molekulárního nahrazení. Obtíže se zdroji záření
takové vlnové délky, aby byla právě za absorpční hranou zvoleného
prvku, lze obejít použitím synchrotronového záření, ale zůstávají
obtíže s vysokou absorbcí v této oblasti.
5. ITERATIVNÍ
METODY ŘEŠENÍ
KRYSTALOVÝCH STRUKTUR
Pod iterativními metodami obvykle rozumíme
metody, které na základě již známého předběžného modelu
části struktury umožňují upřesnění
fází (195) nebo výpočet nových fází (196).
5.1 Metody minimalizace funkce popisující shodu
modelu s experimentem
Mezi tyto metody lze zařadit metodu zkoušek a chyb (197), kdy je tematicky měněn model
struktury a shoda s experimentem je sledována pomocí R –
faktoru (198),
Závislost
R-faktoru na atomových
parametrech je velice komplikovanou funkcí a proto jsou metody tohoto typu
použitelné, pouze podaří-li se redukovat počet neznámých
parametrů na minimum. Známe-li například molekulární geometrii, ale
neznáme umístění molekuly vzhledem k prvkům symetrie,
můžeme vypočítat R-faktory pro
všechny translace s dostatečně velkým krokem – mapu
R – faktorů (199). Místa
s nízkou hodnotou R – faktoru naznačují přibližné hodnoty hledané
polohy molekuly v základní buňce. Výpočet bývá obvykle opakován
s jemnějším krokem a nebo pro další strukturní parametry.
Účinnost metody se podstatně zlepší, zavedeme-li do kriteria shody
další podmínky, které musí pro danou strukturu platit, např.
stereochemické podmínky. Metody tohoto typu mají blízko k metodám zpřesňování
struktury diskutovaném v třetí části Nomenklatury. Zde jsou
uvedeny pouze robustní metody, které dávají jistou naději na konvergenci
do globálního minima.
5.2 Metody opakované Fourierovy
syntézy (200)
Na základě
známého strukturního
fragmentu jsou vypočítány
amplitudy 
a fáze Φ strukturních faktorů, které jsou dále
použity pro výpočet vážené Fourierovy
syntézy (201) s různě
modifikovanými koeficienty, např.
|
|
diferenční syntéza (202) |
(g17) |
|
|
α syntéza
(203) |
(g18) |
|
|
β syntéza
(204) |
(g19) |
|
|
|
(g20) |
|
|
součet
diferenční
a |
(g21) |
kde 
(resp. 
) je
velikost strukturního faktoru určená z experimentu (resp.
výpočtem). Podle některé z těchto map je zpresněn
obraz elektronové hustoty (modifikace
elektronové hustoty (206) a postup je
opakován, dokud není získán uspokojivý obraz struktury. Při tomto
postupu je důležité rozlišit falešná maxima (207)
na Fourierově mapě (slang – duchy) od maxim v místech atomových
poloh na základě apriorní stechiometricé informace.
V případě, že je jako výchozí informace použita poloha malého
počtu silně rozptylujících atomů, užívá se pro tento postup
názvu metoda těžkého atomu (208).
5.3 Molekulární
grafika
Ke studiu složitých molekulárních struktur je
využíváno interaktivní
počítačové grafiky (209)
s možností optimalizovat v reálném
čase (210) překrytí modelu
struktury s maximy na vhodné Fourierově syntéze. Úspěch metody
závisí na tom, zdali se podaří některým z předcházejících
postupů získat dostatečně přesný odhad poloh alespoň
části atomů. Momentální odhad (model) elektronové hustoty je graficky
zobrazen jako třírozměrná Fourierova mapa, jako její rovnoběžná projekce (211) podél zvoleného směru nebo pomocí řezů (212)
Forierovou mapou. Rozložení elektronové hustoty na Fourierově mapě
bývá graficky reprezentováno vrstevnicemi
(213) (tj. čárami spojujícími body
o stejné elektronové hustotě). Dobrý systém musí umožnit okamžitou rotaci molekulárního fragmentu (214) a jeho translaci (215), plynulou změnu
měřítka zobrazení (216) stereoskopický pohled na strukturu, barevné
nebo intensitní zvýraznění částí molekul, interaktivní možnost stavby
molekuly na základě stereochemických představ a výpočtu
geometrie strukturního fragmentu odpovídající minimální energii podle
empirických vztahů užívaných v molekulární
mechanice (217). Dobrý systém umožňuje
i na základě jen částečných údajů o primární, sekundární, terciární
a kvarterní struktuře (218)
makromolekul konstrukci modelu (219) a upřesnění
v přímém prostoru (220). Uživatel přitom musí mít neustále
přehled o chemicky významných
spojeních (chemické konektivitě) (221)
uvnitř fragmentu a o mezimolekulárních
interakcích (222). Nezbytným doplňkem
je zde též metoda izomorfního nahrazení, anomálního rozptylu speciální Fourierovy syntézy (223) a metoda modifikace elektronové
hustoty.
Ze
spřesněného strukturního modelu jsou vypočteny nové, zpravidla
lepší odhady fází strukturních faktorů a celá procedura může
pokračovat některou z metod opakované Fourierovy syntézy.
Při výpočtu je třeba stále sledovat, zdali přidání nových
reflexí s vyšším difrakčním úhlem zlepší obraz struktury. Mezirovinná
vzálenost odpovídající reflexím s nejdelším difrakčním vektorem
a které ještě „zlepšily“ Fourierovou mapu se nazývá rozlíšením (224).
Tento termín tedy udává nejmenší délku rovinných vln z nichž je
vytvořen obraz struktury na Fourierově mapě. Přesnost
stanovení středních poloh atomů bývá o dva řády lepší.
6. EXPERIMENTÁLNÍ URČENÍ FÁZÍ
STRUKTURNÍCH FAKTORŮ
Hodnoty univerzálních strukturních invariantů
lze určit experimentálně na základě vícenásobné difrakce ( 225), tj.
z průběhu intenzity jedné reflexe invariantu při ψ – skanu (226) v těsném
okolí „náběhu“ zbylých
refexí invariantů (s lineárně nezávislými difrakčními
vektory) do difrakční podmínky.
Například triplet lze určit z průběhu
intensity při ψ – skanu
reflexe s difrakčním vektorem
H
v těsném okolí difrakční
podmínky pro difrakční vektor
K.
Na pětikruhovém difraktometru (227)
přitom krystal rotuje kolem vektoru
H v reflexní pomínce tak, aby vektor K
(ale žádný jiný) prošel touž reflexní podmíkou. Na čtyřkruhovém difraktometru (228) je ψ – skan
obvykle simulován řadou
měření 
-skanem pro různá
nastavení krystalu odpovídající vybraným úhlům ψ.
Využití experimentálně
stanovených tripletů je vhodné zejména u obtížně řešitelných struktur, kde je
nutné identifikovat triplety
s hodnotou podstatně odlišnou od 0, π.
Běžnému využití této techniky však brání zejména potřeba malé divergence (229)
primárního svazku záření a z toho vyplývající prodloužené doby
měření více než 10-krát. Různé přístrojové vlivy, absorbce,
tvar vzorku atd. mohou podstatně ovlivnit spolehlivost získaných údajú.
Účinnost metod experimentálního určení fází strukturních faktorů
může být zvýšena využitím synchrotronového
záření (230).
7. JEDNOZNAČNOST URČENÍ KRYSTALOVÉ
STRUKTURY
Za ideálních podmínek je
difrakční obraz jednoznačně určen množinou meziatomových
vektorů a obráceně. Nicméně z praktických
důvodů často volíme vlnovou délku záměrně tak, aby
nedocházelo k anomální disperzi na žádném z atomů struktury
a tedy k vysoké absorpci. Potom však vystupují
meziatomové vektory ve výrazu pro intenzity jen prostřednictvím sudých funkcí (231),
takže není rozlišen jejich směr a nelze od sebe rozlišit homocentrické struktury (232) (viz komentář) se stejnou množinou
meziatomových vektorů.
Speciálním případem
homocentrických struktur jsou enantiomorfní
struktury (233), které mají vzájemně
obrácené směry všech meziatomových vektorů. U centrosymetrických
struktur je centrosymetricky sdružený obraz totožný se vzorem, takže
určení struktury je jednoznačné. U necentrosymetrických struktur
bývá v průběhu řešení struktury náhodně zvolena jedna
z enantiomorfních forem. Až po upřesnění struktury je
rozhodnuto, je-li nutné změnit znaménko všech atomových souřadnic,
či ne, pomocí Bijvoetových
párů (234),
tj. na základě rozdílů
mezi amplitudami komplexně sdružených strukturních faktorů,
u nichž je porušen Friedelův zákon (235)
. Zjištění, která forma
je v krystalu přítomna, je možné též provést pomocí Hamiltonových testů (236), který určí na základě poměru
vážených R faktorů
pravděpodobnost omylu při přijetí hypotézy, že správné
řešení odpovídá nižšímu R
faktoru. Podmínky pro určení absolutní
struktury (237) jsou:
-
struktura nevykazuje pseudosymetrii
(238), neuspořádanost (239), ani dvojčatění
(240);
-
nejde o strukturu, která je „téměř“
centrosymetrická
-
imaginární část
rozptylového faktoru alespoň jednoho
atomu 
.
V principu je tedy struktura
určena difrakčním experimentem jednoznačně. V praxi
však mohou vzniknout obtíže, když přesnost a počet
experimentálně stanovených amplitud strukturních faktorů nejsou
postačující k získaní požadovaného rozlíšení na Fourierově
mapě. U struktur proteinů bývá často obtížné dosáhnout atomárního rozlíšení (241).
Ovšem někdy i u krystalů s méně než sto
symetricky nezávislými atomy mohou nastat komplikace, když krystalová struktura
vykazuje superstrukturní efekty (242), tj. část struktury má vyšší symetrii,
nebo menší základní buňku, než celá struktura.
Při popisu superstrukturních
efektů bývá užíváno předpony „pseudo“, která vyjádřuje odchylky
od ideální symetrie, a dále přídavného jména „nekrystalografický“,
které upozorňuje, že daná operace symetrie platí jen v části
prostoru, a to kvůli tomu, že příslušný prvek symetrie není
krystalografický nebo že je nevhodně umístěn vůči ostatním
prvkům symetrie. Příčinou častých potíží
s vyřešením stuktury bývá nekrystalografická
translační (pseudo-) symetrie (243),
řádu n , tj. když se podobný
strukturní motiv objeví n-krát v téže základní buňce
posunutý vždy o celistvý násobek vektoru
nekrystalografické (pseudo-) translace (244).
Při řešení struktury je
nejprv určena substruktura (245), (tj. část struktury vyhovující vyšší
symetrii, nebo mající menší základní buňku) a teprve poté komplementární struktura (246) odpovídající rozdílu mezi skutečnou
elektronovou hustotou a substrukturou. Elektronová hustota substruktury
přispíva spravidla jen do reflexí odpovídajících supermříži (247)
v reciprokém prostoru. Tyto reflexe jsou nazývány hlavní reflexe (248) (též substrukturní, nevhodně silné reflexe). Ostatní reflexe jsou
označovány jako superstrukturní
reflexe (249) (nevhodně slabé).
Přestože je předem
nerozpoznaná nekrystalografická symetrie
(250) (tj. strukturní fragment má symetrii,
kterou nelze zahrnout do prostorové grupy celého krystalu) zpravidla
příčinou obtíží při určení struktury, může být na
druhé straně značným ulehčením při řešení fázového
problému, pokud ji dovedeme určit předem.
U vrstevnatých struktur (251)
a u struktur, které lze popsat modelem s periodickou poruchou
v geometrii nebo ve složení, tzv. modulovaných
struktur (252) je často nejprve
stanovena tzv. průměrná
struktura (253) a dodatečně
zlepšen popis struktury odvozením a zpřesněním parametrů
popisujících poruchu.
KOMENTÁŘ
x – skan = postupné proměřování nějaké
veličiny v závislosti na proměnné x .
Triple, quartet – zní jako termíny, řekne-li se
trojice, čtverice, každý se okamžitě zeptá „čeho“?
Symetrická minimová funkce – je to dvojznačné, ale
není lepší náhrada. Termín nechce říci, že minimová funkce je symetrická.
Říká, že funkce využívá maxim vzniklých na Pattersonově mapě
díky symetrii.
Zpřesnění = rafinace struktury (labor. slang
odpovídající angl. termínu refinement).
Slovo rafinace upozorňuje, že
jde o přesně definovaný matematický postup. Všimněte si, že
obdobné „čištění ropy“ má jiný význam než „rafinace ropy“. Termín
„zpřesnění struktury“ má tedy tři významy:
1) určení
přesnějších hodnot atomových parametrů některou
z metod minimalizace účelové funkce (refinement of the structure),
2) popis struktury pomocí nových
(lepších) parametrů nebo přidáním nových parametrů dávajících
lepší popis elektronové hustoty,
3) odstranění špatně
umístěných atomů nebo jiných chyb ve strukturním modelu.
Fixace (souřadnicového systému) – vyjadřuje, že se
poloha počátku nemůže změnit, ale nevíme co jsme zvolili.
Vyrovnáváni – fitování (lab. slang odpovídajíci
anglickému termínu) – znamená postupnou změnu jedné funkce tak, aby se
nakonec shodovala s druhou.
Pojem krystalová a molekulární struktura
nebo stručně jenom struktura se použije pouze jde-li
o molekulární krystaly. Všude tam, kde pojem molekuly ztrácí smysl (u
většny anorganických materiálů) mluvíme pouze o krystalové struktuře.
Velikost vektoru = absolutní hodnota vektoru. Nesmí
se v tomto smyslu užívat slova modul.
Modul je základní jednotka, ze které něco skládáme,
nebo pomocí které něco proměřujeme; dělitel při
výpočtu zbytku dělení; konstanta užitá při převodu
logaritmů o různém základu. Je nevhodné používat modul ve smyslu absolutní hodnoty.
Doporučuje se globální minimum místo absolutní minimum, protože je vhodnou
paralelou k termínu lokální minimum.
„Izomorfní nahrazení“ se nám zdá z neznámých
důvodů lepší než „izomorfní
záměna“.
Termín strukturní
amplituda (nebo jednoduše amplituda, pokud nemůže dojít záměně) znamená amplitudu
vlny na Fourierově mapě
odpovídající příspěvku
od struturního faktoru . Užíváme jej tam, kde je třeba vyjádření
pomocí jednoho slova, např. při tvorbě dalších termínů: bazální amplituda, sdružená amplituda
atd. Významově ekvivalentní jsou jednoznačné opisy: „absolutní
hodnota strukturního faktoru“ (zdůrazňující fakt, že je komplexní číslo) a „velikost
strukturního faktoru“ (zdůrazňující vektorové znázornění
).
Slovní spojení homocentrické struktury
implicitně naznačuje pouze stejnou množinu vzdáleností obou struktur,
přestože podle Buergerovy a Hosemanovy definice znamená struktury
s totožnou množinou meziatomových vektorů. Termín izovektorové
struktury byl několikrát použit pro struktury se stejnou množinou
meziatomových vektorů bez ohledu na druh atomů.
Stanovení struktury – implikuje odvození dosud zcela
neznámé struktury. Určení struktury – naznačuje výběr
z několika předpokládaných možností.
Reflexe – (reflexion = reflection) – míní se tím dobře
ohraničený svazek difraktovaného záření, který lze interpretovat jako
odraz od osnovy mřížkových rovin.
Slabá reflexe – unobserved (unsignificant) reflexion – míní se tím
reflexe, u níž je relativní statistická chyba měřené intenzity
větší než stanovený limit. Doporučuje se překlad slabá reflexe (zakazuje se jej používat
ve smyslu superstrukturní reflexe).
Nevhodná synonyma jsou: nepozorovaná reflexe – je
měřená (tedy pozorovaná) zpravidla déle než ostatní; nepozorovatelná
reflexe – při lepším experimentálním zařízení je
pravděpodobně pozorovatelná; nevýznamná reflexe – tyto reflexe
jsou důležité např. pro výpočet normalizovaných strukturních
faktorů.
Pojmy týkající se popisu „nedokonalé symetrie“
v krystalech jsou někdy v různých oblastech krystalografie
definovány odlišně. Tato téma bude podrobně spracována v
některém z nasledujících dílů.
Při tvorbě termínů jsme se
snažili dodržet nasledující pravidla:
konstanta – veličina, která se
nemění za daných okolností,
koeficient – součinitel – konstanta,
kterou se násobí,
faktor – činitel – číslo, nebo výraz, kterým se
násobí,
parametr – proměnná, jejímž prostřednictvím
popisujeme požadované změny (v modelu, funkci a pod.)
člen – číslo, nebo výraz, který
vystupuje v součtu, v řadě, v určité
skupině
položka – člen nějaké skupiny čísel
index – znak připsaný matematickému symbolu
a sloužící k rozlišení prvků stejného druhu
Doporučené značení
Vektor se značí tučnou
kurzívou nebo šípkou nad písmenem 
Je-li vektor užit
jako index, neznačí se
šípkou (např. ).
Tenzor se značí
vlnovkou nad velkým písmenem.
Doporučuje se uvádět spojitou proměnnou
jako funkční závislost (např. ρ(r) ), a proměnnou
nabývající diskrétních hodnot jako index (např. ).
Kromě zápisu difrakčního vektoru bez závorek
a bez čárek je též přípustný i v matematice obvyklý
zápis vektoru (h, k, l), zejména,
pokud by vynechání čárek a závorek mohlo být zdrojem chyb při
přepisu nebo by se zápis stal nepřehledným. Mezera je špatný
„oddělovač“ a zápisy 12 1
3, 1 2 1 3, 1 21 3,
1 2 13, nebo -h1 -h2-k1 -k2-l1 -l2 mohou ve čtenáři vyvolat pochyby. Ke sporu s Millerovou symbolikou
nemůže dojít, protože slovní spojení difrakce na rovině (h, k, l) nemá smysl.
Zkratky
Pokud se nejedná o všeobecně vžitou zkratku
v české a slovenské literatuře, nedoporučuje se užívat
domácích zkratek, (např. metoda vícenásobného izomorfního nahrazení MVIN).
Je-li to třeba, užijte mezinárodní (anglické) zkratky (např. Multiple
Izomorphous Replacement – MIR) i v českém a slovenském
textu. Při prvním výskytu zkratky v textu se ovšem musí uvést plný
anglický termín.