C

Difrakcia rtg. žiarenia na kryštalických látkach

Kinematická teória

Ivan Červeň – Václav Valvoda

1. Rozptyl rtg žiarenia (1)

Pri prechode rtg. žiarenia látkou časť energie primárneho zväzku (2) sa rozptyluje na rozptylových centrách látky, vzniká rozptýlené žiarenie (3). Jeho súčasťou je difraktované žiarenie (4), ďalej žiarenie ktoré vzniká Comptonovým rozptylom (5) (syn. modifikovaný rozptyl (6)) a žiarenie ktoré vzniká pri tepelnom difúznom rozptyle (7). Pri Comptonovom a pri tepelnom difúznom rozptyle ide o nepružný rozptyl (8), pri ktorom sa mení energia fotónov a to v prvom prípade interakciou s elektrónmi, v druhom prípade s kmitmi atómov kryštálu. Pri difrakcii rtg. žiarenia ide o pružný rozptyl (9), pri ktorom sa energia fotónov a vlnová dĺžka žiarenia nemenia. Koherentne rozptýlené vlny pritom navzájom interferujú a v niektorých smeroch, určených vlnovou dĺžkou a priestorovým usporiadaním rozptylových centier, vznikajú difrakčné maximá (10) (syn. difrakcie (11)). Pre ostré difrakčné maximum sa často používa termín reflexia (12), hoci fyzikálne nie je korektný. Energia rozptýlená pri difrakcii sa sústreďuje do difraktovaných zväzkov (13), množina ktorých vytvára v priestore difrakčný obraz (14). Konkrétna registrácia difakčného obrazu je difraktogram (15), (syn. difrakčný záznam (16)), na ktorom sú zachytené difrakčné stopy (17), alebo difrakčné čiary (18) (difrakčné línie).

Rtg. žiarenie sa rozptyľuje v podstate len na elektrónoch látky, ale za rozptylové centrá (19) je vhodné v niektorých súvislostiach považovať atómy, molekuly, prípadne základné bunky kryštálu.

2. Amplitúda difraktovaných elektromagnetických vĺn

Amplitúda vlny pružne rozptýlenej jedným elektrónom závisí od amplitúdy dopadajúcej vlny, vzdialenosti od rozptylujúceho elektrónu a od rozptylového uhla (20), čo je uhol medzi uvažovaným smerom postupu rozptýlenej vlny a smerom dopadajúcej (primárnej) vlny. Pri opise difrakcie sa častejšie používa difrakčný uhol (21) (syn. Braggov uhol (22), označenie Q), ktorý sa rovná polovici rozptylového uhla.

Amplitúda výslednej vlny, zloženej z vĺn koherentne rozptýlených viacerými rozptylovými centrami rozptylujúceho objektu, je amplitúda rozptylu (23) tohto objektu:

kde A _j je amplitúda vlny prichádzajúcej od rozptylového centra s polohovým vektorom r_j , k_o a k sú vlnové vektory (24) dopadajúcej a rozptýlenej vlny, je difrakčný vektor (25). Ako difrakčný vektor sa niekedy označuje aj vektor , ktorému potom prislúcha veľkosť , kde je vlnová dĺžka dopadajúcej i rozptýlenej vlny rtg. žiarenia.

Amplitúda rozptylu podľa vzťahu (c1) je vyjadrená v absolútnych jednotkách (26). Ak ju vydelíme amplitúdou vlny pružne rozptýlenej v tom istom smere jedným elektrónom, dostaneme bezrozmernú veličinu – amplitúdu rozptylu v elektrónových jednotkách (27).

Rozptyl rtg. žiarenia izolovaným atómom, považovaným za rozptylové centrum, sa charakterizuje atómovým rozptylovým faktorom (28) (skrátene atómový faktor (29), ozačenie f (S )), čo je amplitúda rozptylu na atóme vyjadrená v elektrónových jednotkách. Súčet podľa vzťahu (c1) cez elektróny atómu sa v tomto prípade nahrádza integráciou:

kde je elektrónová hustota (30) v atóme, ktorá vyjadruje počet elektrónov pripadajúci na objemovú jednotku (ako funkcia polohy v atóme). Atómový faktor, ako vidno zo vzťahu (c2), je vo všeobecnosti komplexné číslo. V prípade sféricky symetrických atómov a ďaleko od rezonančných frekvencií je to reálne číslo, vyjadrujúce, koľkokrát je amplitúda rozptylu na atóme (ióne) väčšia, než amplitúda rozptylu na jednom elektróne v tom istom smere.

Súčasťou atómového faktora je korekcia na anomálnu disperziu (31), ktorá sa skladá z reálnej (32) a z imaginárnej časti (33), čím sa zohľadňuje interakcia rtg. žiarenia s atómom v oblasti jeho rezonančných frekvencií (34). Imaginárna časť korekcie adobúda maximálnu hodnotu pri rezonančnej absorpcii (35).

Amplitúda rozptylu na skupine N atómov sa v elektrónových jednotkách vyjadruje súčtom

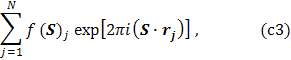
ktorý je správny, keď atómy sú nepohyblivé. Tepelné kmity (36) individuálnych atómov sa zohľadňujú teplotným faktorom (37) (syn Debyeov - Wallerov faktor (38)),

kde je stredná kvadratická výchylka (39) j-teho atómu z rovnovážnej polohy a  je teplotný parameter (40) (syn. Debyeov parameter (41)). Anizotropné kmitanie atómov sa v exponente teplotného faktora vyjadrujú tenzorovou veličinou, ktorej súradnice nazývame anizotropné teplotné parametre (42).

Výraz predstavujúci amplitúdu rozptylu na atómoch základnej bunky kryštálu, vyjadrený v elektrónových jednotkách, a zohľadňujúci aj tepelné kmitanie atómov, je štruktúrny faktor (43):

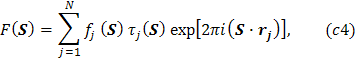
kde n je počet atómov pripadajúci na základnú bunku. Štruktúrny faktor je podľa (c4) komplexné číslo, ktoré sa zapisuje aj v tvare , kde je fázový uhol (44) (skrátene fáza (45)) a F absolútna hodnota (46) (modul (47)) štruktúrneho faktora. Výpočet štruktúrneho faktora sa dá zjednodušiť použitím faktorov symetrie (48)

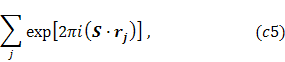
pričom sumácia prebieha cez všetky polohy, ktoré sú symetricky ekvivalentné s vybranou polohou.

Štruktúrny faktor možno vyjadriť aj ako Fourierovu transformáciu (49) elektrónovej hustoty :

teda vzťahom podobným vzťahu (c2), s tým rozdielom, že treba integrovať cez celý objem základnej bunky. Vzhľadom na to, že elektrónová hustota je trojrozmerne periodická funkcia, možno ju vyjadriť pomocou trojrozmerného Fourierovho radu (50).

Ak má kryštál tvar hranola s  základnými bunkami (sú celé čísla), jeho amplitúda rozptylu v elektrónových jednotkách sa dá vyjadriť súčinom , kde F(S) je štruktúrny faktor a mriežkový faktor (51) (syn. geometrický faktor (52)):

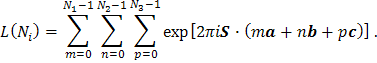
Amplitúda rozptylu kryštálu konečných rozmerov ľubovolného tvaru sa dá vyjariť ako konvolúcia (53) Fourierovej transformácie elektrónovej hustoty a Fourierovej transformácie tvarovej funkcie (54) kryštálu, pričom tvarová funkcia má v kryštáli hodnotu 1, mimo neho hodnotu 0.

3. Difrakčné podmienky

Smery, ktorými sa môžu šíriť zväzky difraktovaných lúčov pri difrakcii na usporiadanom kryštáli, sú určené difrakčnými podmienkami (55). Dajú sa vyjadriť niekoľkými spôsobmi.

Laueho rovnice (56) vyjadrujú súvislosť medzi základnými vektormi a, b, c priestorovej mriežky a difrakčným vektorom S :

a × S = h , b × S = k , c × S = l (c7),

kde čísla h, k, l sú difrakčné indexy (57) (syn. Laueho indexy (58)). Difrakčné indexy – na rozdiel od Millerových indexov – môžu byť súdeliteľné a ich spoločný deliteľ sa nazýva rád difrakcie (59). Laueho podmienky sú splnené, keď difrakčný vektor S , ktorý v nich vystupuje,

spĺňa podmienku, že je mriežkovým vektorom recipročnej miežky, pričom jeho súradnicami sú práve difrakčné indexy:

Podmienka (c8) je rovnocenná s Laueho rovnicami a je základom geometrickej Ewaldovej konštrukcie (60) smerov difrakčných maxím. Pritom sa využíva Ewaldova guľová plocha (61) (reflexná guľová plocha (62)), s polomerom 1/l a limitujúca guľová plocha (63) s dvojnásobným polomerom, ktorá v recipročnom priestore vymedzuje maximále možné hodnoty difrakčných indexov pre rôzne polohy kryštálu.

Difrakčnou podmienkou rovnocennou s Laueho rovnicami je aj Braggova rovnica (64)

(c9),

kde je vlnová dĺžka, difrakčný uhol a medzirovinná vzdialenosť.

4. Intenzita difraktovaného žiarenia

Intenzita difraktovaného žiarenia (65) je množstvo energie, ktoré prenáša difraktované žiarenie v sledovanom smere za jednotku času cez jednotku plochy. Energia súvisiaca s konkrétnou difrakciou sa šíri konečným priestorovým uhlom. Integrál intenzity difraktovaného žiarenia cez príslušný priestorový uhol je integrálna intenzita (66). Je to skalárna veličina, zhodná s tokom energie.

Pri meraniach na kryštáloch, ktoré sa otáčajú uhlovou rýchlosťou w, sa používajú veličiny integrálna odrazivosť (67), definovaná výrazom a integrálna reflexná mohutnosť (68) definovaná vzťahom , kde je celková energia prislúchajúca difrakcii hkl počas doby merania, intenzita a tok energie primárneho zväzku rtg žiarenia.

Intenzitu rtg. žiarenia pružne rozptýleného jedným elektrónom vyjadruje Thomsonov vzťah (69)

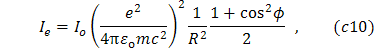
kde je intenzita primárneho nepolarizovaného zväzku rtg. žiarenia, R vzdialenosť od elektrónu a rozptylový uhol.

Intenzita žiarenia difraktovaného skupinou atómov je úmerná štvorcu modulu príslušnej amplitúdy rozptylu. Ak ju vydelíme intenzitou žiarenia pružne rozptýleného (v tom istom smere), dostaneme intenzitu vyjadrenú v elektrónových jednotkách.

Intenzita difraktovaného žiarenia je ovplyvňovaná rôznymi faktormi:

Lorentzov faktor (70) zohľadňuje veľkosť časového intervalu, počas ktorého je pre uvažovanú osnovu rovín reálneho kryštálu splnená difrakčná podmienka, čo závisí od experimentálnej metódy.

Faktor násobnosti (71) udáva počet osnov kryštalograficky ekvivalentných rovín, ktoré pri danej experimentálnej metóde poskytujú koincidenčné difrakčné stopy.

Absorpčný faktor (72) zohľadňuje absorpciu primárneho i difraktovaného žiarenia pri prechode kryštálom a závisí od zloženia a hustoty kryštálu, jeho tvaru, rozmerov a vlnovej dĺžky rtg. žiarenia.

Polarizačný faktor (73) zohľadňuje čiastočnú polarizáciu rtg. žiarenia pri difrakcii.

Ak látka pozostáva z relatívne samostatných a v priestore náhodne orientovaných molekúl (plyn, kvapalina), potom štvorec modulu amplytúdy rozptylu v elektrónových jednotkách sa vyjadruje Debyeovou rozptylovou rovnicou (74)

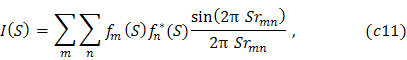
kde je vzdialenosť medzi m-tým a  n-tým atómom molekuly, a   atómové faktory a S veľkosť difrakčného vektora.

Intenzita difraktovaného žiarenia každej základnej bunky kryštálu, a tým aj celého kryštálu, je úmerná druhej mocnine modulu štruktúrneho faktora . Priradením tejto hodnoty mriežkovému bodu recipročnej mriežky so súradnicami h, k, l , vznikne vážená recipročná mriežka (75).

Pre usporiadaný kryštál, ktorý má tvar kvádra obsahujúceho základných buniek, je intenzita difraktovaného žiarenia úmerná súčinu

kde F(S) je štruktúrny faktor, S difrakčný vektor a výraz v hranatej zátvorke interferenčná funkcia (76), ktorá má nenulové hodnoty prakticky len pre vetory S spĺňajúce difrakčné podmienky, t.j. v prípade, keď vo vzťahu (c12) namiesto všeobecného výrazu F(S) možno písať F(hkl). Podľa Friedelovho zákona (77) platí rovnosť , kde predstavujú difrakčné indexy tzv. Bijvoetových párov (78) difrakcií. Preto je vážená recipročná mriežka centrosymetrická a jej symetria je opísaná jednou z jedenástich Laueho grúp (79) symetrie. Z difrakčného hľadiska sa preto kryštály zaraďujú do jedného z jedenástich Laueho oddelení symetrie (80).

Difrakčný symbol (81) sa skladá zo symbolu Laueho grupy, za ktorým nasleduje extinkčný symbol (82), vyjadrujúci typ centrácie mriežky a prítomnosť prvkov symetrie spôsobujúcich systematické vyhasínanie difrakcií (83) (skrutkové osi, sklzné roviny). Z priestorovej grupy sa dajú odvodiť reflexné podmienky (84), t.j. dovolené kombinácie difrakčných indexov pre výskyt difrakčných maxím. Veľmi slabé difrakcie, ktoré sa môžu objaviť v miestach systematicy vyhasínajúcich difrakcií v dôsledku asymetrickej deformácie nábojovej hustoty alebo asymetrických kmitov atómov, sa nazývajú takmer zakázané difrakcie (85). Inou príčinou systematicky vyhasínajúcich difrakcií môžu byť násobné difrakcie (86) – Renningerov jav (87). Pri štúdiu usporiadania naďaleko zostáva intenzita základných difrakcií (88) nezmenená, zatiaľ čo intenzita nadštruktúrnych difrakcií (89) klesá s rastúcim stupňom neusporiadanosti.

5. Kinematická a dynamická teória difrakcie

Kinematická teória difrakcie (90) opisuje difrakciu ako jednorázový akt rozptylu. Nezohľadňuje možnosť opätovnej difrakcie počas prechodu difrakovaného žiarenia látkou, počíta len s postupným zoslabovaním intenzity primárneho a difraktovaného zväzku vplyvom absorpcie. Dynamická teória difrakcie (91) počíta jednak s touto možnosťou, ale aj s interferenciou medzi viackrát difraktovanými vlnami ako aj medzi difraktovanými vlnami a primárnou vlnou. Obidva tieto tzv. dynamické javy (92) zapríčiňujú zoslabenie intenzity difraktovaného žiarenia, nazývaného extinkcia (93). Prejavujú sa najmä pri kryštáloch väčšej hrúbky a súvisia aj s ich mozaikovou štruktúrou (94).

Primárna extinkcia (95) predstavuje zoslabenie intenzity difraktovaného žiarenia vplyvom dynamických javov v jednotlivých blokoch mozaikového kryštálu. Sekundárna extinkcia (96) súvisí s odtienením mozaikových blokov nachádzajúcich sa v hĺbke kryštálu blokmi na jeho povrchu. Primárna a sekundárna extinkcia sa kvantitatívne charakterizujú koeficientom extinkcie (97).

Vzhľadom na dynamické javy pri difrakcii sa kryštály delia na dve skupiny. Ideálne dokonalé kryštály (98) majú celý svoj objem vyplnený jedinou koherentnou oblasťou (99). Mozaikové kryštály (100) predstavujú agregát mozaikových blokov (101) obyčajne menších než 10^-2 mm, navzájom dezorientovaných o uhlové sekundy až stupne. Ak má kryštál dostatočne malé mozaikové bloky, na ktorých nedochádza k primárnej extinkcii, a pritom náhodne orientované s dostatočným uhlovým rozptylom aby nedochádzalo k interferencii vĺn difraktovaných rôznymi blokmi, ide o ideálne mozaikový kryštál (102), nazývaný aj ideálne nedokonalý kryštál (103).

Komentár

Predložený text sa obmedzuje na kinematickú teóriu difrakcie, ale v závere sú uvedené a vzájomne porovnané východiskové predpoklady kinematickej a dynamickej teórie.Dynamickej teórii je venovaná osobitná časť.

Počas prípravy textu sa vyskytli niekedy až protichodné názory posudzovateľov, týkajúce sa fundamentálnych termínov súvisiacich s difrakciou.

Nejednotný názor sa prejavil na obsah a vzájomný vzťah termínov rozptyl – dfrakcia. Podľa jedného názoru treba pod difrakciou rozumieť len vznik ostrých maxím, všetko ostatné je rozptyl. V texte sme sa priklonili k názoru, podľa ktorého rozptyl je pre difrakciu nadradeným pojmom, charakterizujúcim jav, pri ktorom dochádza k zmene smeru šírenia vĺn. V tomto duchu sa používa aj medzinárodne akceptovaný a používaný termín atómový rozptylový faktor. Termín difrakcia, tak ako je uvedený v texte, umožňuje hovoriť o difrakcii aj na amorfných látkach, kvapalinách alebo veľmi malých kryštáloch.

Rozdielne názory boli aj na používanie termínov difrakcia – reflexia. V texte sme sa priklonili k fyzikálne správnemu termínu difrakcia, pričom tento termín treba chápať len ako skrátenú verziu úplného termínu difrakčné maximum. Terminologicky totiž nie je správne, ak sa jeden termín – difrakcia – používa v dvoch významoch, raz pre fyzikálny jav, inokedy pre konkrétne difrakčné maximum. Termín reflexia, napriek fyzikálnej nevhodnosti, je natoľko zaužívaný, že nie je možné ho ignorovať. Formulácia týkajúca sa reflexie je prevzatá z Cowleyovej monografie Diffraction Physics. Citovať však treba aj názor J. Kuběnu, ktor upozornil, že rtg. žiarenie sa na rozhraní dvoch prostredí skutočne aj odráža, a že termín reflexia by sa mal používať len v tejto súvislosti.

Text sa zaoberá len rtg. žiarením, ale keď išlo o jeho vlnové prejavy, používali sme termín vlnenie, resp. vlna. Vo fyzikálnej literatúre je ustálené spojenie amplitúda vlny, a nie amplitúda žiarenia. Na druhej strane sa však používa spojenie intenzita žiarenia, čo sme v texte rešpektovali.

Termín atómový fakor treba chápať len ako skrátenú, i keď často používanú formu úplného termínu atómový rozptylový faktor, vystihujúceho len jednu z množstva vlastností atómu. Skrátená forma je vhodná, keď nemôže dôjsť k omylu.

„Amplitúdu rozptylu chápeme ako komplexné číslo. Týka sa to aj štruktúrneho faktora, pre ktorý niektorí autori používajú termín štruktúrna amplitúda“ (Cowley). Iní autori pod štruktúrnou amplitúdou rozumejú len modul štruktúrneho faktora (Kraus). V texte sme sa priklonili k termínom podľa Medzinárodných tabuliek.

V súvislosti s Ewaldovou konštrukciou sme použili termín guľová plocha, teda nie guľa či sféra, lebo v podstate len tá je relevantná z hľadiska určenia smerov difrakčných maxím.

V texte sme sa snažili pridŕžať termínov, ktoré boli použité v rozličných knižných publikáciách, či skriptách, osobitne Chemického náučného slovníka I., ktorý vydala ALFA, Bratislava 1983.